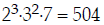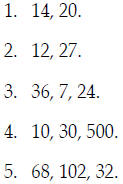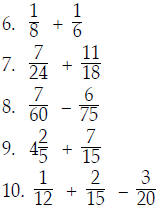Adding fractions using the Least Common Denominator
Next we multiply these together. Here's the result of the
third step:
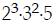
The result of this multiplication is the LCD. Multiplied out, we get 360.
So, the LCD of 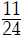 and
and
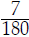 is
is
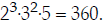
• Having the LCD in factored form is very useful. We will
see why when we actually
add fractions using this method.
Let's try this with our previous example:
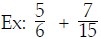
This time, we will find and use the LCD.
Step 1: 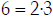
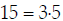
Step 2: 2, 3, 5
Step 3: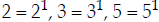 . (The highest
power of each factor is only 1,
. (The highest
power of each factor is only 1,
which we don't need to write.)
Now multiply each factor together:
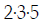
The LCD is 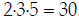 . (That's the end of the LCD
process.)
. (That's the end of the LCD
process.)
Next we convert the fractions to the same denominator. We will make use of the
fact
that the denominators and the LCD are already factored. To convert 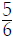 to a fraction
to a fraction
with the LCD in the bottom, compare the factorization of
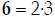 to the
to the 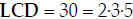 .
.
The LCD has a factor of 5 that 6 doesn't have (all other factors of 6 and the
LCD are the
same). So we multiply the fraction 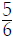 (top and
bottom) by 5:
(top and
bottom) by 5:
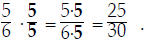
Next compare 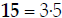 (the
denominator of
(the
denominator of
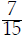 ) to the
) to the 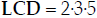 .
.
The LCD has a "2" that 15 doesn't have. So we multiply top and bottom by 2:
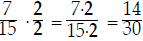
Now we've converted the fractions; the last step is to add
them together:
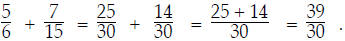
Notice that the answer we get,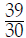 , can still be reduced:
, can still be reduced: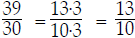 .
.
The numbers we had to work with during the addition were
smaller than the numbers
we had to consider the first time we did this problem; and in both cases, we
still had to
factor in order to simplify the fraction. But by using the LCD, we only
had to factor
smaller numbers.
Here's an example where we find the LCD of three fractions:
Ex: 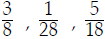 . Find the LCD of all three fractions (we
won't do the addition).
. Find the LCD of all three fractions (we
won't do the addition).
Step 1:
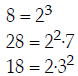
Step 2: 2, 3, 7
Step 3: 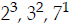 . (Each factor raised to its
highest power.) Then multiply:
. (Each factor raised to its
highest power.) Then multiply:
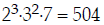
The LCD is 504. (Finished!)
Finally, notice that the LCD of two or more fractions is always the smallest
number that
can be evenly divided by the denominators of the fractions. For example, 504 is
divisible
by each of the numbers 8, 28, and 18; and no smaller number can be divided by
all
three. In other words, the LCD is also the least common multiple (LCM) of the
denominators of the fractions. The LCD
of 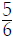 and
and
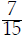 is 30; the LCM of the
numbers 6 and 15 is also 30.
is 30; the LCM of the
numbers 6 and 15 is also 30.
You should try all of the following:
EXERCISES.
Find the least common multiple of the
given numbers using the LCD process. |
In problems 6 - 10, add or subtract the
fractions by converting to the LCD. |
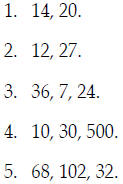 |
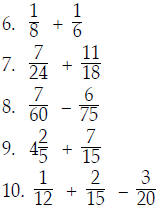 |
Some thoughts on studying mathematics and being
successful, or
"The Eleven Steps to a Good Grade In Math"
1) Take good, complete class notes, employing the lecture outline as a
guide.
2) Plan to spend about two hours on each assignment. You may sometimes need to
spend more.
3) As soon after the class section as possible, study your class notes
and examples. You
may even want to rewrite your notes for greater clarity. (This rewrite process
serves
to make you begin thinking about the ideas, the first step in learning.)
4) Then read carefully the section(s) of the textbook related to the
material, giving
special attention to the vocabulary, basic concepts and problem examples. You
may
want to relate this reading to your class notes, highlighting the concepts which
have
been discussed.
5) Now begin the assignment. (To do so earlier is foolhardy, since the
assignment is
designed to be practice and application of the ideas and concepts, which you
really
need to grasp and understand before you do the assignment; hence, prior study of
the ideas is essential!)
6) Check your answers in the back of the textbook as you go along. If you
are having
difficulties, go back and restudy, looking at the examples done in class and in
the
textbook for similarities to your problem; then try your problem again.
7) If problems arise at this point, and you are unable to work them out for
yourself or
with one another (group study is encouraged - we can learn from each other's
problems and analyses), then the time has come to seek help. Attend the
problem
session before the next class, or if that is impossible, seek help directly
form the
instructor during office hours. Do not wait until the next class to ask the
question;
there may not be time, or we may not be able to get to your problem.
8) When you have successfully completed your assignment, go back and reread
the
text sections and class notes again, for emphasis and review of the
concepts. This
won’t take very long, but it pays big dividends in locking in the concepts,
processes,
and terminology into your "memory bank."
9) Successful students find that the next step in doing one's assignment is to look
ahead at what is coming up in the next class; you can easily see what
section we will
be discussing by looking at your syllabus. Do a quick read over of the
appropriate
text sections, not for mastery but for general overview. Get familiar with the
new
terms and basic concepts, so when they are presented in class they wont seem so
"foreign" to you.
10) Finally, successful students also have found that, just prior to the next
class (perhaps
fifteen minutes before class begins, or even on the way to class) a quick
reread of
the "old" class notes as well as the "new" text section gives them an edge,
especially
if there is a quiz (announced or unannounced).
11) One final suggestion: don't get discouraged, and above all don't give up
too easily.
Mathematics is challenging, but it can also be fun, interesting, intellectually
rewarding, and very useful!


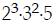
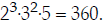
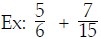
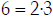
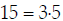
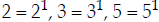 . (The highest
power of each factor is only 1,
. (The highest
power of each factor is only 1,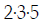
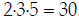 . (That's the end of the LCD
process.)
. (That's the end of the LCD
process.)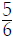 to a fraction
to a fraction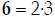 to the
to the 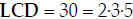 .
.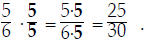
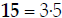 (the
denominator of
(the
denominator of
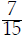 ) to the
) to the 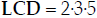 .
.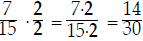
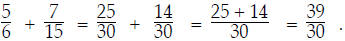
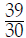 , can still be reduced:
, can still be reduced: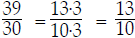 .
.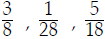 . Find the LCD of all three fractions (we
won't do the addition).
. Find the LCD of all three fractions (we
won't do the addition).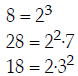
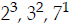 . (Each factor raised to its
highest power.) Then multiply:
. (Each factor raised to its
highest power.) Then multiply: