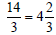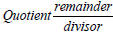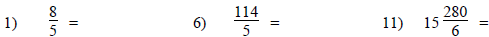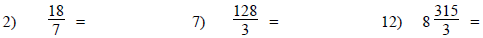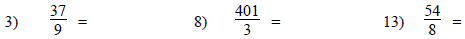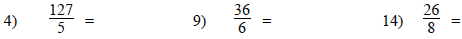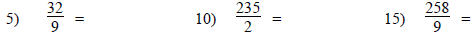Fraction Competency Packet
To use this booklet, review the glossary, study the
examples, then
work through the exercises. The answers are at the end of the
booklet. When you find an unfamiliar word, check the glossary for
a definition or explanation.
Calculators are not allowed when taking the Computerized
Placement Test (CPT), nor in Fundamentals of Mathematics, Pre-
Algebra, and Elementary Algebra; therefore, do not rely on a
calculator when working the problems in this booklet.
If you have difficulty understanding any of the concepts, come to
one of the Tutoring Centers located on the Lynn, Danvers Main
and Danvers Hathorne Campuses. Hours are available at (978)
762-4000 x 5410. The Centers are closed when school is not in
session, and Summer hours are limited.
Glossary
Boosting: Rewriting a fraction as an equivalent fraction with a higher
denominator.
Denominator: Bottom number of a fraction indicating how many parts make a
whole.
Difference: The result when two numbers are subtracted.
Divisor: The number after the division sign in a division problem, (i.e.
12÷7); or the bottom
number of a fraction, (i.e.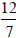 ); the number
"outside" the division house (i.e.
); the number
"outside" the division house (i.e. 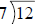 ).
).
Equivalent Fraction: Fractions that are found by multiplying the numerators
and
denominators by the same number.
Factor: Numbers equal to or less than a given number that divides the
number evenly. For
example, the factors of 12 are 1, 2, 3, 4, 6, 12.
Fraction: Any number written in the form of one whole number over
another, 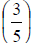 , indicating
, indicating
number of parts being considered over the number of parts that make one whole.
Fraction Bar: The line separating the numerator and denominator in a
fraction, and it indicates
division.
Greatest Common Factor (GCF): The largest matching factor of two or more
given numbers.
It is used to reduce fractions.
Improper Fraction: Any fraction with the numerator larger than the
denominator.
Least Common Denominator (LCD): The smallest matching multiple of two or
more given
numbers. It is used to "boost" fractions. (Also called Least Common Multiple,
LCM)
Mixed Number: A whole number and a fraction. (It implies addition of
wholes and parts; that
is, 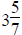 is read "three and five sevenths".)
is read "three and five sevenths".)
Multiple: (Similar to the "times table.") A multiple of a given number is
equal to the given
number or greater. Multiples are found by multiplying the given number in turn
by 1, 2,
3,... For example, multiples of 4 are 4, 8, 12, 16, …
Numerator: The top number of a fraction. It indicates how many parts of a
certain size are
represented.
Prime Factor: Factors of a number that are only divisible by 1 and the
given number. For
example, prime factors of 12 are 1 x 2 x 2 x 3. Some frequently used Prime
Numbers are 2,
3, 5, 7, 11, 13.
Product: The result when two numbers are multiplied.
Proper Fraction: Any fraction when the numerator is
less than the denominator.
Quotient: The solution to a division problem.
Reducing:
Dividing the numerator and the denominator by the same number to get an
equivalent fraction. Final answers of most fraction problems should be expressed
reduced to “simplest terms”; in other words, the numerator and denominator have
no
more common factors.
Remainder:
The number left after a whole number division problem is complete. When
converting an improper fraction to a mixed number, the remainder is the
numerator of the
fraction.
Sum: the result when two numbers are added.
Whole Number: The Numbers system including 0, 1, 2, 3,….
General Fraction Information

 The fraction that
represents the above picture is
The fraction that
represents the above picture is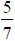 and is read
“five sevenths”. That means
and is read
“five sevenths”. That means
that five of the parts are shaded, and it would take seven parts of that size to
make a whole.
 One whole can be "cut up" into equal size
parts; therefore,
One whole can be "cut up" into equal size
parts; therefore, 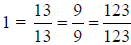 , etc.
, etc.
 A whole number can be written as a fraction
with a denominator of 1; for example,
A whole number can be written as a fraction
with a denominator of 1; for example, 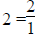 .
.
Zero can be written as a fraction using zero as the numerator and any whole
number as the
denominator, for example,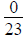 .
.
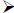 Any whole number may be written as a mixed number by using a zero fraction.
For example,
Any whole number may be written as a mixed number by using a zero fraction.
For example,
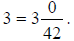
Mixed Numbers
To convert a mixed number,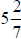 , to an improper fraction, , to an improper fraction,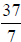 : :
|
Whole Number |
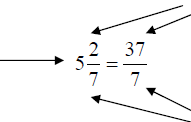 |
Numerator |
|
Denominator |
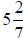 |
Work in a clockwise direction, beginning with
the
denominator, (7). |
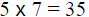 |
Multiply the denominator (7) by the whole
number,
(5) |
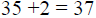 |
Add that product, (35), to the numerator (2)
of the
fraction. |
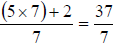 |
The denominator remains the same for the
mixed
number and the improper fraction. |
|
Convert to Improper Fractions:
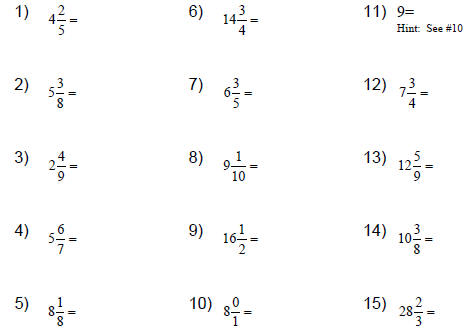
Find the equivalent fractions as indicated:
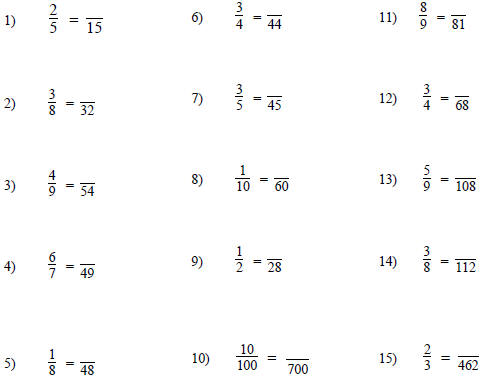
Equivalent Fractions with Smaller Denominators
Reducing Fractions
Example: Reduce the following fraction to lowest terms
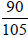
There are three common methods, DO NOT mix steps of the methods! |
Method 1:
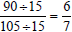 |
The Greatest Common Factor for 90 and 105 is
15. Divide the
numerator and the denominator by the GCF, 15. |
|
Method 2:
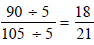 |
Examine the numerator and denominator for any common
factors, divide both numerator and denominator by that
common factor. Repeat as needed. |
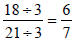 |
 Both 90 and 105 are divisible by 5. Both 90 and 105 are divisible by 5.
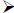 Both 18 and 21 are divisible by 3. Both 18 and 21 are divisible by 3. |
|
Method 3:
 |
Express the numerator and denominator as a
product of prime
factors. |
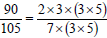 |
Divide numerator and denominator by common
factors, (3x5) |
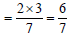 |
Multiply remaining factors. |
|
Reduce these fractions.
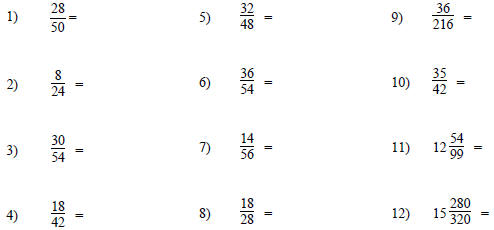
Convert these improper fractions to mixed numbers. Be sure
to reduce when it’s
possible.
#11, 12 Hint: how many
wholes will there be?
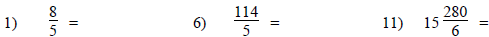
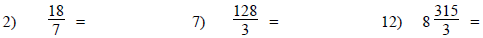
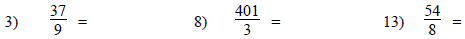
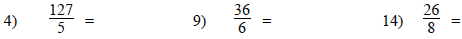
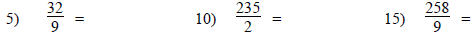


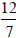 ); the number
"outside" the division house (i.e.
); the number
"outside" the division house (i.e. 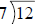 ).
).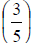 , indicating
, indicating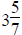 is read "three and five sevenths".)
is read "three and five sevenths".)
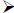 The fraction that
represents the above picture is
The fraction that
represents the above picture is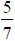 and is read
“five sevenths”. That means
and is read
“five sevenths”. That means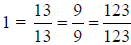 , etc.
, etc.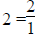 .
.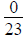 .
.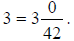
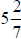 , to an improper fraction,
, to an improper fraction,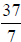 :
: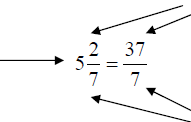
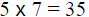
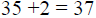
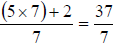
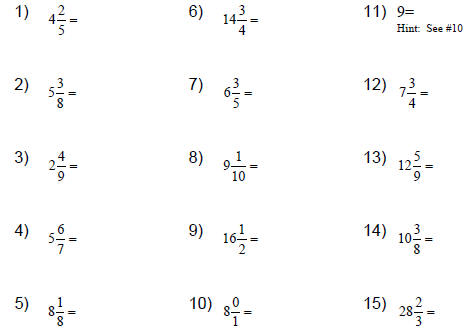
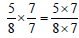
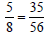
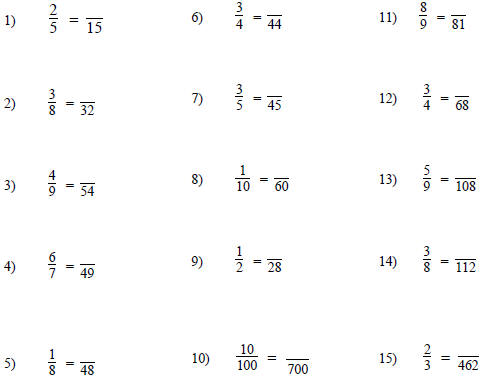
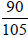
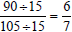
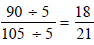
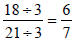
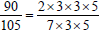
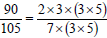
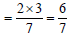
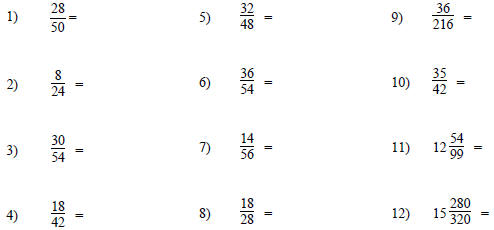
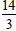 to an Improper Fraction
to an Improper Fraction