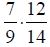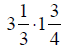Fractions
 Learn the definition
of factor.
Learn the definition
of factor.
 Write fractions in lowest terms.
Write fractions in lowest terms.
 Multiply and divide fractions.
Multiply and divide fractions.
 Add and subtract fractions.
Add and subtract fractions.
 Solve applied problems that involve
Solve applied problems that involve
fractions.
 Interpret data in a circle graph.
Interpret data in a circle graph.
Definitions
Natural numbers:1, 2, 3, 4,…,
Whole numbers: 0, 1, 2, 3, 4,…,
Fractions: 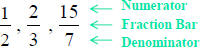
Proper fraction: has a value of less then 1; the
numerator
is smaller than or equal to the denominator.
Improper fraction: has a value of greater then 1; the
numerator is larger than the denominator.
Mixed number: is a combination of a whole number and a
fraction.
Ex. The improper fraction 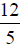 can be written
can be written
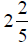 , a mixed number.
, a mixed number.
Objective
Learn the definition of factor.
In the statement 2 ×9 = 18, the numbers 2 and 9 are called
factors. Other factors of 18 include 1, 3, 6, and 18. The number
18 in this statement is called a product.
The number 18 is factored by writing it as a product of two or
more numbers.
Ex. 6 ·3, 18 ×1, (2)(9), or 2(3)(3)
A natural number greater than 1 is prime if its products
include only 1 and itself.
Ex. 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37,…
A natural number greater than 1 that is not prime is
called a
composite number.
Ex. 4, 6, 8, 9, 10, 12,…
EXAMPLE 1
Factoring Numbers
Write 90 as the product of prime factors.
Solution:
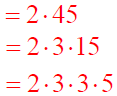
Starting with the smallest prime factor is not necessary.
No matter
which prime factor is started with the same prime factorization will
always be found.
Objective

Writing fractions in lowest terms.
A fraction is in lowest terms, when the numerator
and
denominator have no common factors other than 1.
Basic Principle of Fractions:
If the numerator and denominator are multiplied or
divided by the same nonzero number, the fraction remains
unchanged.
Writing a Fraction in Lowest Terms:
Step 1:
Write the numerator and the denominator as the
product of prime factors.
Step 2:
Divide the numerator and denominator by the
greatest common factor, the product of all
factors common to both.
EXAMPLE 2
Writing Fractions in Lowest
Terms
Write 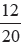 in lowest terms
in lowest terms
Solution:
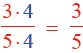
When writing fractions in lowest terms, be sure to
include the factor 1 in the numerator or an error may
result.
Objective

Multiply and divide fractions.
Multiplying Fractions:
If 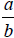 and
and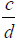 are fractions, then
are fractions, then 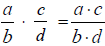 ,
,
That is, to multiply two fractions, multiply their
numerators
and then multiply their denominators.
Dividing Fractions :
If
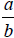 and
and
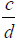 are fractions, then
are fractions, then
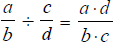 .
.
That is, to divide two fractions, is to multiply its
reciprocal;
the fraction flipped upside down.
EXAMPLE 3
Multiplying Fractions
Find each product, and write it in lowest simple terms.
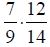
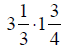


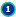 Learn the definition
of factor.
Learn the definition
of factor. Write fractions in lowest terms.
Write fractions in lowest terms. Multiply and divide fractions.
Multiply and divide fractions. Add and subtract fractions.
Add and subtract fractions. Solve applied problems that involve
Solve applied problems that involve  Interpret data in a circle graph.
Interpret data in a circle graph.
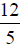 can be written
can be written
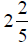 , a mixed number.
, a mixed number.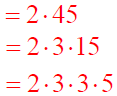
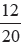 in lowest terms
in lowest terms
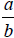 and
and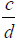 are fractions, then
are fractions, then 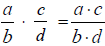 ,
,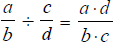 .
.