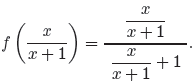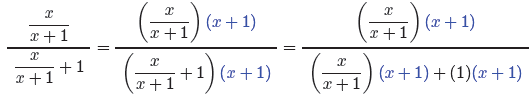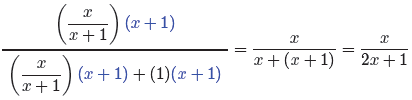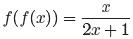Complex Fractions
In this section we learn how to simplify what are called
complex fractions, an example
of which follows.
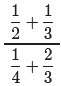 (1)
(1)
Note that both the numerator and denominator are fraction problems in their own
right, lending credence to why we refer to such a structure as a “complex
fraction.”
There are two very different techniques we can use to simplify the complex
fraction
(1). The first technique is a “natural” choice.
Simplifying Complex Fractions — First Technique. To
simplify a complex
fraction, proceed as follows:
1. Simplify the numerator.
2. Simplify the denominator.
3. Simplify the division problem that remains.
Let’s follow this outline to simplify the complex fraction
(1). First, add the fractions
in the numerator as follows.
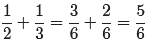 (2)
(2)
Secondly, add the fractions in the denominator as follows.
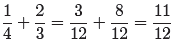 (3)
(3)
Substitute the results from (2) and (3) into the numerator and
denominator of (1),
respectively.
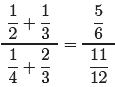 (4)
(4)
The right-hand side of (4) is equivalent to
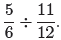
This is a division problem, so invert and multiply, factor, then cancel common
factors.
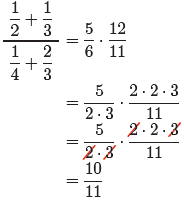
Here is an arrangement of the work, from start to finish, presented without
comment.
This is a good template to emulate when doing your homework.
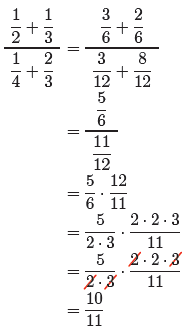
Now, let’s look at a second approach to the problem. We saw that simplifying the
numerator in (2) required a common denominator of 6. Simplifying the
denominator in
(3) required a common denominator of 12. So, let’s choose another common
denominator,
this one a common denominator for both numerator and denominator, namely, 12.
Now, multiply top and bottom (numerator and denominator) of the complex fraction
(1) by 12, as follows.
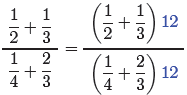 (5)
(5)
Distribute the 12 in both numerator and denominator and simplify.
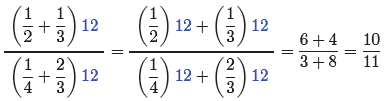
Let’s summarize this second technique.
Simplifying Complex Fractions — Second Technique. To
simplify a complex
fraction, proceed as follows:1. Find a common
denominator for both numerator and denominator.
2. Clear fractions from the numerator and denomaintor by multiplying each by
the common denominator found in the first step.
Note that for this particular problem, the second method
is much more efficient. It
saves both space and time and is more aesthetically pleasing. It is the
technique that
we will favor in the rest of this section.
Let’s look at another example.
 Example 6. Use both
the First and Second Techniques to simplify the expression
Example 6. Use both
the First and Second Techniques to simplify the expression
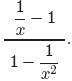 (7)
(7)
State all restrictions.
Let’s use the first technique, simplifying numerator and
denominator separately
before dividing. First, make equivalent fractions with a common denominator for
the
subtraction problem in the numerator of (7) and simplify. Do the same for
the denominator.
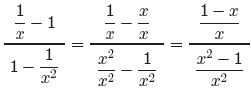
Next, invert and multiply, then factor.
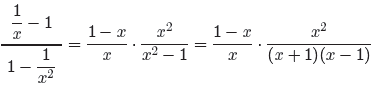
Let’s invoke the sign change rule and negate two parts of the fraction (1 −
x)/x, numerator
and fraction bar, then cancel the common factors.
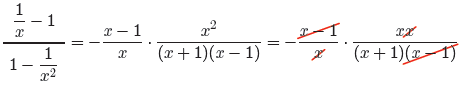
Hence,
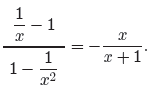
Now, let’s try the problem a second time, multiplying numerator and denominator
by x2 to clear fractions from both the numerator and denominator.
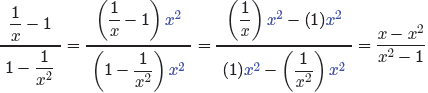
The order in the numerator of the last fraction intimates that a sign change
would be
helpful. Negate the numerator and fraction bar, factor, then cancel common
factors.
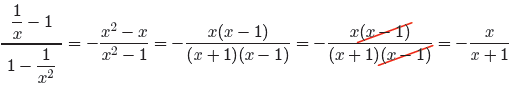
This is precisely the same answer found with the first technique. To list the
restrictions,
we must make sure that no values of x make any denominator equal to zero, at the
beginning of the problem, in the body of our work, or in the final answer.
In the original problem, if x = 0, then both 1/x and 1/x2
are undefined, so x = 0
is a restriction. In the body of our work, the factors x + 1 and x − 1 found in
various
denominators make x = −1 and x = 1 restrictions. No other denominators supply
restrictions that have not already been listed. Hence, for all x other than −1,
0, and
1, the left-hand side of
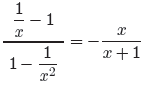 (8)
(8)
is identical to the right-hand side. Again, the calculator’s table utility
provides ample
evidence of this fact in the screenshots shown in Figure 1.
Note the ERR (error) messages at each of the restricted values of x, but also
note
the perfect agreement of Y1 and Y2 at all other values of x.
Let’s look at another example, an important example involving function notation.
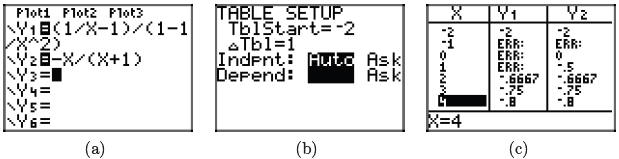
Figure 1. Using the table feature of the graphing calculator to check the
identity in (8).
 Example 9. Given that
Example 9. Given that
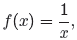
simplify the expression
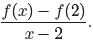
List all restrictions.
Remember, f(2) means substitute 2 for x. Because f(x) = 1/x, we know that
f(2) = 1/2, so
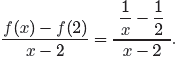
To clear the fractions from the numerator, we’d use a common denominator of 2x.
There
are no fractions in the denominator that need clearing, so the common
denominator
for numerator and denominator is 2x. Multiply numerator and denominator by 2x.
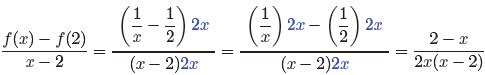
Negate the numerator and fraction bar, then cancel common factors.
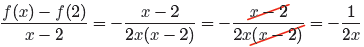
In the original problem, we have a denominator of x − 2, so x = 2 is a
restriction. If
the body of our work, there is a fraction 1/x, which is undefined when x = 0, so
x = 0
is also a restriction. The remaining denominators provide no other restrictions.
Hence,
for all values of x except 0 and 2, the left-hand side of
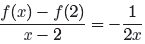
is identical to the right-hand side.
Let’s look at another example involving function notation.
 Example 10. Given
Example 10. Given
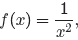
simplify the expression
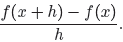 (11)
(11)
List all restrictions.
The function notation f(x + h) is asking us to replace each instance of x in the
formula 1/x2 with x + h. Thus, f(x + h) = 1/(x + h)2.
Here is another way to think of this substitution. Suppose that we remove the x
from
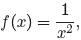
so that it reads
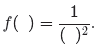 (12)
(12)
Now, if you want to compute f(2), simply insert a 2 in the blank area between
parentheses.
In our case, we want to compute f(x + h), so we insert an x + h in the blank
space between parentheses in (12) to get
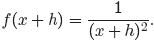
With these preliminary remarks in mind, let’s return to the problem. First, we
interpret the function notation as in our preliminary remarks and write
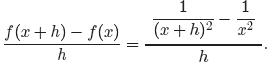
The common denominator for the numerator is found by listing each factor to the
highest power that it occurs. Hence, the common denominator is x2(x + h)2. The
denominator has no fractions to be cleared, so it suffices to multiply both
numerator
and denominator by x2(x + h)2.
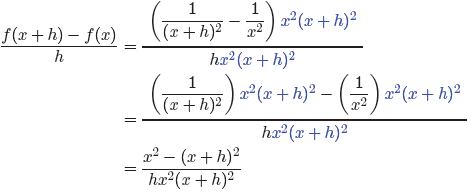
We will now expand the numerator. Don’t forget to use parentheses and distribute
that minus sign.
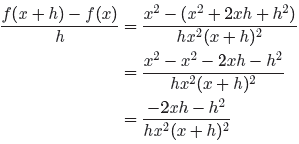
Finally, factor a −h out of the numerator in hopes of finding a common factor to
cancel.
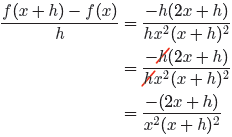
We must now discuss the restrictions. In the original question (11), the
h in the
denominator must not equal zero. Hence, h = 0 is a restriction. In the final
simplified
form, the factor of x2 in the denominator is undefined if x = 0. Hence, x = 0
is
a restriction. Finally, the factor of (x + h)2 in the final denominator is
undefined if
x+h = 0, so x = −h is a restriction. The remaining denominators provide no
additional
restrictions. Hence, provided h ≠ 0, x ≠ 0, and x ≠ −h, for all other
combinations of
x and h, the left-hand side of
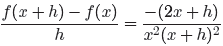
is identical to the right-hand side.
Let’s look at one final example using function notation.
 Example 13. If
Example 13. If
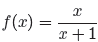 (14)
(14)
simplify f(f(x)).
We first evaluate f at x, then evaluate f at the result of the first
computation.
Thus, we work the inner function first to obtain
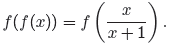
The notation f(x/(x + 1)) is asking us to replace each occurrence of x in the
formula
x/(x + 1) with the expression x/(x + 1). Confusing? Here is an easy way to think
of
this substitution. Suppose that we remove x from
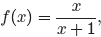
replacing each occurrence of x with empty parentheses, which will produce the
template
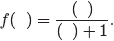 (15)
(15)
Now, if asked to compute f(3), simply insert 3 into the blank areas between
parentheses.
In this case, we want to compute f(x/(x+1)), so we insert x/(x+1) in the blank
space
between each set of parentheses in (15) to obtain
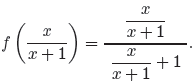
We now have a complex fraction. The common denominator for both top and bottom
of this complex fraction is x + 1. Thus, we multiply both numerator and
denominator
of our complex fraction by x + 1 and use the distributive property as follows.
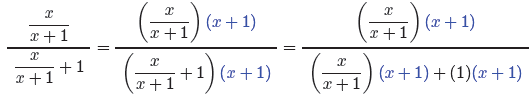
Cancel and simplify.
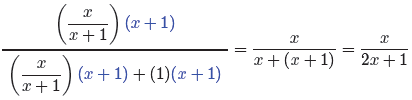
In the final denominator, the value x = −1/2 makes the denominator 2x + 1 equal
to zero. Hence, x = −1/2 is a restriction. In the body of our work, several
fractions
have denominators of x + 1 and are therefore undefined at x = −1. Thus, x = −1
is a
restriction. No other denominators add additional restrictions.
Hence, for all values of x, except x = −1/2 and x = −1, the left-hand side of
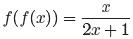
is identical to the right-hand side.


 (1)
(1) (2)
(2)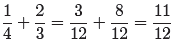 (3)
(3)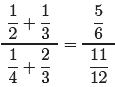 (4)
(4)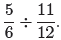
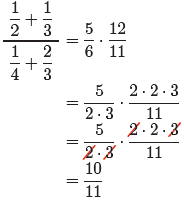
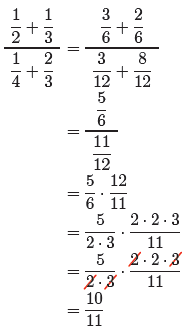
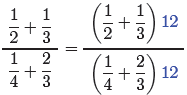 (5)
(5)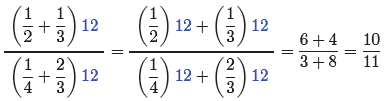
 Example 6. Use both
the First and Second Techniques to simplify the expression
Example 6. Use both
the First and Second Techniques to simplify the expression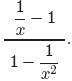 (7)
(7)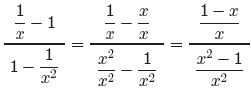
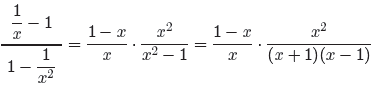
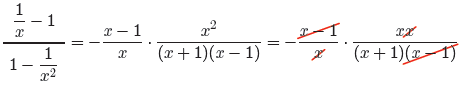
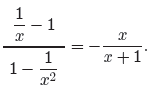
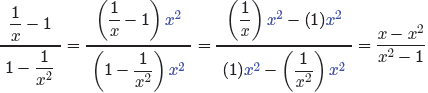
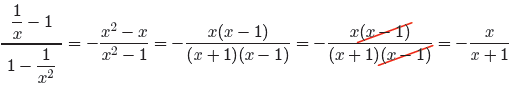
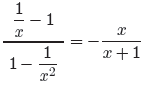 (8)
(8)
 Example 9. Given that
Example 9. Given that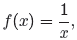
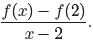
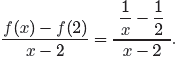
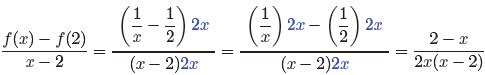
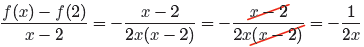
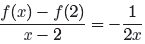
 Example 10. Given
Example 10. Given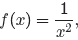
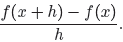 (11)
(11)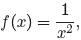
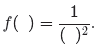 (12)
(12)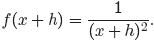
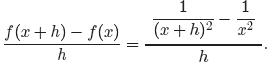
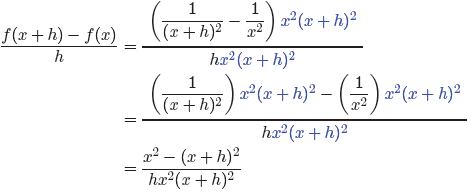
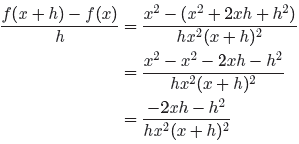
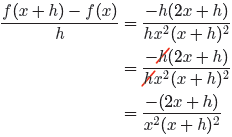
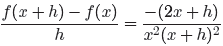
 Example 13. If
Example 13. If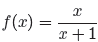 (14)
(14)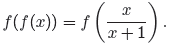
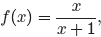
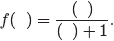 (15)
(15)