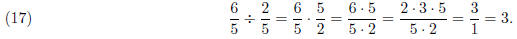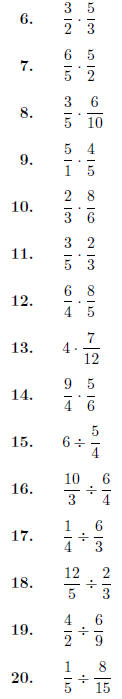|
Home |
Multiplication of FractionsKeep in mind that the division bar in a fraction indicates
division. For example,(1) If the division doesn’t come out evenly, we generally just
leave the division problem as a fraction. Keep in mind also that division and multiplicaton go
together well, and as a result, multiplying and dividing
Since we can reverse a multiplication without affecting
the answer, we say that multiplication is commutative. and since multiplication is commutative, we have
Suppose we want to multiply two fractions. For example, consider
We have two numbers on top, the 2 and the 5, and these are
to be multiplied. We have two numbers on the We can just multiply the 2 and 5, then divide by the 3 and
4. We generally end up multiplying the tops and
We’ll talk about reducing fractions in a bit. Don’t worry about that now. 1. Quiz 03, Part I
2. Reducing fractions Reducing fractions works by doing a
multiplication backwards. For example, in the following, we can factor
In the second step, we can see that we’re multiplying by a
2 and dividing by a 2.
Since we’re multiplying by 5 and dividing by 5, that’s the
same as multiplying by 1.
We’re multiplying by a 2 and 3, and we’re dividing by a 2 and 3. 3. Dividing by fractions Consider the example
Since dividing by 5 is the same as multiplying by 1/5 , we can rewrite this as a multiplication.
On the other hand, if we’re dividing by a fraction, this
involves dividing by a division. In general, we just invert the fraction that we’re dividing by.
It works the same way when we have a fraction with
fractions inside. The middle fraction bar is just another
It’s customary to reduce any fractions you get as an answer.
4. Quiz 03, Part II
For the rest of these problems, multiply or divide, and
then reduce as much as you can.
5. Homework 03
For the rest of these problems, multiply or divide, and then reduce as much as you can.
|












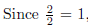 that’s the
that’s the