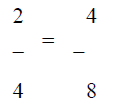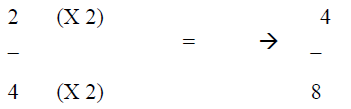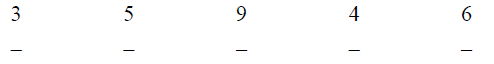Fabulous Fractions

Day 2

Lesson
Exploring Equivalent Fractions

Objectives
Students will be able to express what fractions are equivalent fractions.
Students will be able to explain why the fractions are equivalent.

Standards
Strand -> Number Sense and Operations
Standard -> Students will understand meanings of operations and procedures, and
how they relate to one another.

Materials
Fraction Bars
Overhead Fraction Bars
Mathematics journals

Opening Activity
Give the students the following scenario: Jamie has a Butterfinger. His mother is
making him split the candy bar with his little brother. Jamie told his brother that he
would give him 2/4 of the candy bar, is this half of the candy bar? Ask the
students for their response and have them explain their reasoning.

Main Activity
Pass the sheets of fraction bars out to the class. I will then have each student
separate each fraction bar from the sheet of fraction bars, then pass the sheet to
the next student. I will explain that fractions are a part of the whole and that each
student is holding a fraction or a part of the whole set of fraction bars. I will then
have the students who are holding green fraction bars (halves) stand up and say
what fractional value of the whole they have. Next I will have the students who
have the black fraction bars (tenths) stand up. They will state what fractional
value of the whole they each have. The students who are standing will then
compare their fractional bars with each other. As they are doing this, they should
notice that even though the purple is broken up differently than the green, they
both have the same value. The class will be able to see this because when you line
the two fraction bars up, green next to purple, the shaded portions are equal. I will
then have the people who are holding the yellow fraction bars (thirds) stand up.
They will follow the same exact steps that were taken by the students who were
holding the green and black cards. This time the students who are holding the red
fraction bars (sixths) will be paired up with these students.

Now that they understand that equivalent fractions exist, I will show them the
mathematical procedure to find equivalent fractions. I will explain to them that
whatever they do to the numerator, they have to do to the denominator in order to
find an equivalent fraction. It does not matter what the value of the number is,
they have to make sure and do the same action to both the numerator and
denominator. Go through a couple of examples on the board with the students.

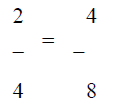
Explain to them that you multiplied the numerator by 2 (2 X 2) to get 4. You
multiplied the denominator by 2 (4 X 2) to get 8. So now the new equivalent
fraction is 4/8.

Show the students the work on the board of how you obtained your answer. So
write out the multiplication.

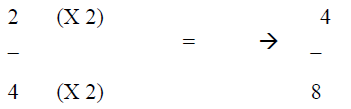
Ask the students to give you examples of equivalent fractions to 2/4.

Write the following examples on the board and have one student come up to each
problem and write an equivalent fraction to the example. Once that student has
completed one example have the student select another student to come up to the
board and complete the next problem. The rest of the class should be copying the
problems along with the solutions to the problems. Once they have completed the
five examples on the board, they will then go back and find another equivalent
fraction for each of the problems.

Examples:

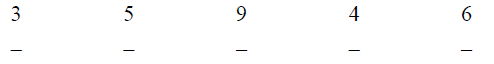
Closing Activity
I will then write another fraction on the board. On a sheet of paper have the
students copy down the fraction. They will then have to give three equivalent
fractions for the fraction that was given.

Homework
In their mathematics journals, have the students state in words how to find
equivalent fractions.

ANSWER KEY

Homework
Below is a possible homework response in their mathematics journal that would receive full credit.

In order to find equivalent fractions, you have to multiply both the numerator and the
denominator by the same number. If you do not use the same number, you will not get equivalent
fractions.

Day 3

Lesson
Reducing / simplifying fractions

Objectives
Students will be able to reduce / simplify fractions.
Students will be able to compare decimal values to find equivalences.

Standards
Strand -> Number Sense and Operations
Standard -> Students will understand meanings of operations and procedures, and
how they relate to one another.

Materials
TI – 73 Graphing calculator
Index cards
Markers
Rainbow fraction circles
Worksheet -> ‘My Fraction Cards’

Opening Activity
Ask the students if they would want to have 2/8 or 4/16 of the cake? Have the
students raise their hands to which portion they would rather have of the cake.
Ask the students to explain their reasoning behind choosing which portion they
want of the cake.

Main Activity
After listening to the student’s responses take out the rainbow fraction circles and
put them on the overhead. Take out the 2/8 and 4/16 rainbow fraction circles.
Place them side by side and ask the students the same question. See their
responses and then ask for explanations of why they think what they think. They
should be able to tell you that they are equal.

Now put up on the overhead some examples of fractions, such as 2/4 and 4/12.
Explain to them that they are going to be simplifying fractions. In order to simplify
a fraction, the numerator and denominator have to be divisible by the same
number. A easy way to figure out what number goes into both numbers is to list each numbers factors.

Find the factors of 4 and 12.
4 = 1, 2, and 4
12 = 1, 2, 3, 4, 6, and 12

Now compare the factors and find all the numbers that each number has in
common. 2 and 4 are in both factors of the numbers. Explain to them that you can
use either number, but to find the fraction in simplest form, use the biggest
common factor.

Now divide each part of the fraction by the common factor. You must divide the
numerator and denominator by the SAME number. So 4 / 4 = 1 and 12 / 4 = 3. So
now the reduced fraction will be 1/3.

4/12 = 1/3

Now give them another example but this time pick a fraction that is already
reduced. Tell them to go through the same process and simplify the fraction. The
students will then realize that if a fraction can not be reduced, there will be not
common factors between the two numbers.

Explain to the students that they can check to see if they have correctly reduced
each fraction by using a calculator. They can compute each fraction on the
calculator and compare the decimal values to determine if they have reduced the
fraction correctly.

Have the students get into groups of 4. Hand out the pre-made fraction cards that
are on the index cards and worksheet entitled ‘My Fraction Cards’. Explain to
them that each card has a fraction on one side, and they need to simplify the
fraction, and then find the equivalent fraction to the reduced fraction. There will
be 15 cards in each packet and they are to write each fraction index card down on
the worksheet.

Examples of fraction cards are below . . .

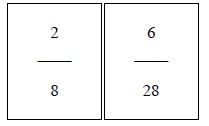
The worksheet will have the students reducing and finding one equivalent fraction.

Closing Activity

Ticket out of the door -> in order for the students to leave the classroom, I will
write two fractions on the board. The students will have to reduce each fraction
and write two equivalent fractions for each.

Homework

Have each group switch their cards with another group. Have the students write
down the other group’s fractions on their worksheets. Have them complete the
worksheet. Next day in class have the students compare with the group that they
switched cards with to see if they have the correct answers.

My Fraction Cards

Directions -> Write each fraction from your index card in the column entitled ‘Fraction Card’. In
the next column, reduce each fraction to simplest form. In the last column, find two equivalent
fractions.

Fraction Card	Simplest / Reduced Fraction Form	Equivalent Fractions ( 2 )

On the back of this worksheet I would have the same table as above so they could compute the
other group’s fraction cards for homework.