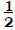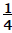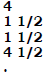Fractions, Ratios, Money, Decimals and Percent
Teacher: How many equal parts make up this whole?
Students: Two.
Teacher: Does anyone know what we call each of the equal parts?
Student: A half.
If no one knows, we teach the name to use.
Teacher: There are two parts. We write the fraction for one part like this:
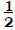
The bottom number is how many equal pieces together make up the whole. The top
number is the
number of pieces that we have.
(illustration 11-1-13)
(S-5 square with four S-3 squares next to it formed into a square the same
shape.)
Teacher: How many equal parts make up this whole?
Students: Four.
Teacher: Does anyone know what we call each of the equal parts?
Student: Fourths.
If no one knows, we teach the name to use.
Teacher: Here's the fraction for a fourth.
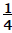
What does the bottom number mean?
Student: How many pieces to make the whole.
Teacher: What does the top number mean?
Student: That's for the one little piece.
Teacher: Let's try another one.
We do not worry about reducing fractions to their lowest denominators. We leave
2/4 as 2/4 for now.
Proving blocks...
High school students learn about axioms, theorems and proofs in geometry. An
axiom is a statement
that is accepted as true without proof. A theorem is a statement that can be
proved.
Axiom: The S-1 square has an area of one.
Theorem: Find the areas of the other shapes. Keep a record of your proofs.
Each proven area is a theorem that follows from the axiom.
New axiom: The T-1 triangle has an area of one.
When the axiom is changed, do the theorems change as well?
Power Blocks provide our students a background for
understanding fractions regardless of the child's
age. The beginning understandings of fractions come from the questions we ask
and the experiences
that the materials provide. There are no rules to memorize. There are no
workbook pages to fill out.
Power Blocks are proving blocks. We define the problem. Our students seek out
answers and prove
the answers that they find. The lesson might be called fractions, geometry, or
free exploring with the
blocks. The lesson's name does not limit the learning being done.
Lesson Two
| Purpose |
Learn to find areas of shapes on geoboards. Learn
to prove
the areas of found shapes. |
| Summary |
Students make shapes on their geoboards and learn
specific
techniques for proving areas. Areas of triangles are searched
specifically for patterns. |
| Materials |
Geoboards, geoboard recording paper; paper
triangles and
squares or Power Blocks for proofs. |
| Topic |
Make shapes with areas of 2 1/2 and prove areas. |
| Topic |
Make shapes with areas of 3 1/2 and prove areas. |
| Topic |
Make shapes with areas of any size and prove
areas. |
| Topic |
Make right triangles and prove areas. |
| Topic |
Find areas for and search for patterns in
triangles with bases
on the bottom row. |
| Homework |
If geoboards can be sent home, finding areas of
shapes is
continued there. |
Two and one-half...
Geoboards are an excellent material for teaching the geometry of shape.
Geoboards are an excellent
material for teaching fractional values of shapes, as well. But geoboards did
not help Ryan, Hayley, or
Jill make sense of shape or area (Beginning Number, Lesson Eight and Geometry,
Lesson Two).
Power Blocks are a readiness material for geoboards. Power Blocks give children
the background for
understanding the shapes and the fractions of shapes they construct on geoboards.
Power Blocks are
Lesson One. Geoboards are Lesson Two.
Teacher: See if you can make shapes with areas of two and one-half square
units on your
geoboard. Use your square and triangle pieces of paper or use your Power Block
pieces to
prove the areas of the shapes that you create.
(illustration 11-2-1)
(Show a few different ways of making two and one-half square units. Put both the
square and triangle
paper and different size Power Block proofs along side each geoboard shape.)
In Beginning Number, Lesson Eight, (page 000), we asked our students to find
ways to make shapes on
their geoboards with areas of twos, threes and more. We find areas on geoboards
by adding or
subtracting wholes and halves. Our students added and subtracted fractions and
whole numbers,
even though we had not reached the point in this book where fractions were
taught. Chapter titles and
lesson numbers are not meant to limit what or when we teach.
Teacher: Please record the shapes you discover, so that you can keep images
of the shapes you are
inventing, even when you run out of room on your geoboard.
(illustration 11-2-2)
(Student recorded geoboard designs on paper. Label each shape "2 1/2".)
As our students work, we roam around the room asking individual children to
prove the areas of their
shapes to us. They also prove their shapes to one another.
Teacher: Prove the area each shape that you think has an area of two and
one-half to your
neighbor before you record it on your paper.
If your neighbor agrees with your proof, then your neighbor must sign his or her
name next to
your drawing.
If your neighbor does not accept your proof, then raise your hand and I will
help you both decide
if your proof is sufficient.
Students checking students means thirty teachers for every
child in the room.
Three and one-half...
Teacher: Now, see if you can make shapes with areas of three and one-half square
units on your
geoboard. Please prove the area to your neighbor before recording it on your
paper. Please
also write the number of the area inside the shape.
(illustration 11-2-3)
(Student recorded geoboard designs on paper. Label each shape "3 1/2".)
Beginning Number, Lesson Eight...
If we presented all of Beginning Number, Lesson Eight to our students, then we
have already asked our
students to find areas for any geoboard shape they might create. If we have not
already asked, the time
to ask is now. We may look back at Lesson Eight (page 000) to see examples of
area-finding methods
our students might employ.
Teacher: Work with a partner to see what kinds of shapes you can make on your
geoboard for
which you can prove the area. You may make shapes for any area you can prove.
Finding areas for any kind of shape is a fraction lesson automatically.
(illustration 11-2-4)
(Student recorded geoboard designs for a variety of shapes on paper. Label each
shape with its proven
area.)
As our students work, we walk around the room, sharing everyone's strategies for
proofs.
Right triangles...
Teacher: Today I want you to see how many different right triangles you can find
areas for.
Right triangles are triangles with a right angle in them. (Geometry, Lesson
Seven, page 000.)
The rule for the right triangles is that the base for each new triangle you make
has to be on
the bottom row of nails on your geoboard. Please record the triangles you make
and the areas
that you find.
(illustration 11-2-5)
(All the right triangles are made with their bases on the bottom row of the
geoboard. Give one example
of a triangle made with its base n o t on the bottom row and add in the caption
that this is not allowed.
Demonstrate with the Power Blocks that right triangles are half of rectangles or
squares. Then show on
the geoboard right triangles as halves of rectangles or squares. Show a
recording sheet with the areas
written inside the triangles. All of the triangles on the recording sheet should
have their bases on the
bottom line of the recording area.)
Teacher: Let's see if we can find a pattern in the areas of the triangles you
have made that might
help us predict the areas for triangles not yet made.
For each area that you find, please write numbers for the height, the base and
the area of the
triangle on your chalkboard and hold it up for me to see. You already know how
to find the
number for the area. Find the number for the base and number for the height by
counting the
spaces and not the nails.
(illustration 11-2-6)
(Show geoboard examples of what is meant by base and height and counting
spaces.)
Teacher: I'll record each new set of numbers on the overhead. Please look to see
if I already have
the numbers for your triangle written on the overhead before you write your
numbers on your
board.
Will our students see the pattern? Will they see that area
is found by multiplying the base times the
height and dividing the resulting number in half? Can we be patient enough to
wait until they do?
Not right...
Teacher: What is the height of these triangles?
(illustration 11-2-7)
(Show one acute triangle and one obtuse triangle. Show that, for the acute
triangle, the height is the
perpendicular line from the base to the highest point. Show that, for the obtuse
triangle, the height is
also the perpendicular line from the base to the highest point, but we need to
extend the base beyond
the triangle to find that perpendicular point. The height is how tall the
triangle is, straight up from the
line the base is on.)