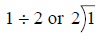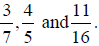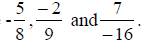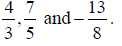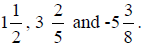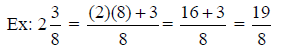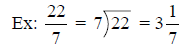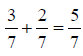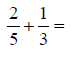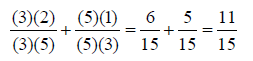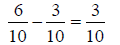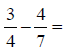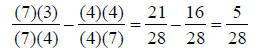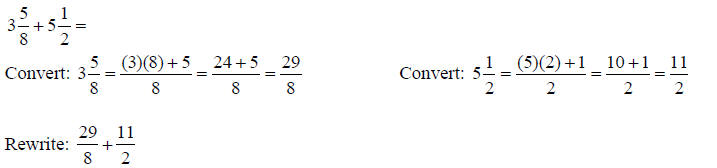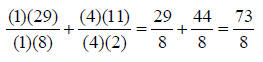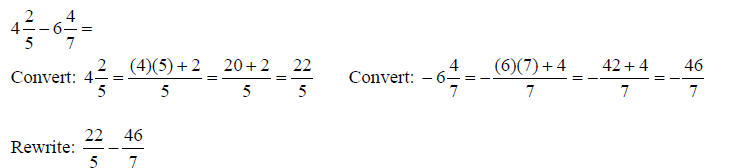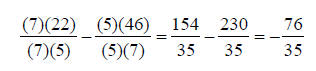|
Home |
FractionsNumbers such as 1/2, 1/4 and 1/3 are fractions. When dealing with fractions, the top number is called the
numerator and the bottom number is 1 numerator When solving fractions, the numerator is being divided by the denominator.
There are a few different types of fractions including
proper fractions, improper fractions and When the denominator is greater than the numerator, it is
considered a proper fraction.
Fractions can also be negative numbers like
When the denominator is smaller than the numerator, it is
considered an improper fraction.
When there is a whole number and a fraction, it is
considered a mixed number.
To convert a mixed number to an improper fraction,
multiply the whole number by the
To convert an improper fraction to a mixed number, divide
the numerator by the denominator.
Adding and Subtracting FractionsIf fractions have the same denominator, the numerators can
be added together. The An Example:
If fractions do not have the same denominator, a common
multiple of the denominators must be A common multiple can be defined as any number that is
divisible by two different values. In An Example:
The multiples of 5 are 1 x 5 = 5, 2 x 5 = 10, 3 x 5 = 15, 4 x 5 = 20, 5 x 5 = 25 … The multiples of 3 are 1 x 3 = 3, 2 x 3 = 6, 3 x 3 = 9, 3 x 4 = 12, 3 x 5 = 15, 3 x 6 = 18 … A common multiple of 3 and 5 is 15. The numerator and the denominator of each fraction must be
multiplied by the same number in
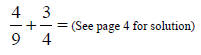
1) Try this example:
Subtracting Fractions:Subtracting fractions is very similar to adding fractions.
When subtracting fractions with An Example:
If fractions do not have the same denominator, a common
multiple of the denominators must be An Example:
The multiples of 4 are: 1 x 4 = 4, 2 x 4 = 8, 3 x 4 = 12,
4 x 4 = 16, 5 x 4 = 20, 6 x 4 = 24, A common multiple of 4 and 7 is 28. The numerator and the denominator of each fraction must be
multiplied by the same number in
2) Try this example:
Adding and Subtracting Mixed NumbersTo add and subtract mixed numbers, the first step is to
convert the mixed numbers to improper An Example:
The multiples of 8 are: 1x 8 = 8, 2 x 8 = 16, 3 x 8 = 24… The common multiple of 8 and 2 is 8. The fraction 29/8 has
an 8 in the denominator; therefore a
An Example:
The multiples of 5 are 1 x 5 = 5, 2 x 5 = 10, 3 x 5 = 15,
4 x 5 = 20, 5 x 5 = 25, 6 x 5 = 30, The common multiple of 5 and 7 is 35.
3) Try this example:
|