Complex Fractions

1 Complex Fractions

Goal: Simplify complex fractions. Up to now, we are only able to manipulate
simple fractions, meaning the numerator and the denominator are all polyno-
mials or numbers.

Definition A complex fraction is a fraction where the numerator, denominator,
or both contain a fraction.

Example

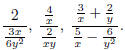
1.1 Method I

To Simplify a Complex Fraction by Multiplying by a Common Denominator

• 1. Find the least common denominator (LCD) of all fractions appearing
within the complex fraction.

• 2. Multiply both the numerator and the denominator of the complex
fraction by the LCD of the complex fraction from step 1.

• 3. Simplify whenever possible.

Example Simplify the complex fraction

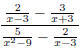
1.2 Method II

To Simplify a Complex Fraction by Simplifying the Numerator and Denominator

• 1. Create one single fraction in the numerator (if necessary).

• 2. Create one single fraction in the denominator (if necessary).

• 3. Remember the main fraction line means "divide". Rewrite the fraction
using a division symbol .

• 4. Follow the normal rules for dividing fractions: Invert the the second
term (the denominator of the complex fraction) and multiply (by the nu-
merator of the complex fraction).

• 5. Simplify if needed.

Example

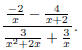
Remark Complex Fractions are EASY to simplify if you remember that the
main fraction bar means DIVIDE.

To manipulate complex fractions, just convert them to simple fractions.
Then use the rules for simple fractions.

Example Simplify and subtract:

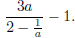
Example Simplify and add:

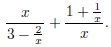
2 Homework # 3

Problem set 4.4, 16-36(odd numbers), 40-60(even numbers).