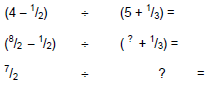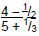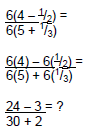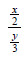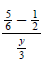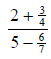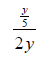|
Home |
Complex FractionsObjective Module 8A: Pre-LectureA complex fraction is a fraction containing one or more fractions in the numerator or denominator or both the numerator and denominator. Examine the following examples of complex fractions from Arithmetic and Algebra to understand the definition clearly:
The fraction bar represents division, so each of the above examples can also be written as a division problem:
To solve these problems, we must follow the rules for adding, subtracting, multiplying and dividing fractions AND follow the Order of Operations. 1. There are four steps in the Order of Operations. Each
step must be done in order, from left to right. What are the four steps? 2. The complex fraction Order of Operations requires that expressions within parentheses be simplified first. Since we must have the same denominators to add and subtract fractions, we can rewrite 4 and 5: 4 = 4/1 = 8/2 and 5 = ?/1 = ?/3. So we have
To finish the solution, follow the rule for division of fractions. Write the rule for division of fractions and complete the solution to the problem. ________________________________________________________________ ________________________________________________________________ ________________________________________________________________ 3. It is clear that the mastery of operations with fractions is important in solving complex fractions. Consider a different problem-solving strategy: Go back to the original complex fraction:
Find the least common denominator of all the fractions in
the complex fraction: Use the Distributive Property of Multiplication over Addition to multiply both the numerator and denominator of the complex fraction by the LCD:
Finish the solution. Using this strategy correctly, you will get the same answer as in #2. 4. There are two basic strategies that can be used to simplify complex fractions: Strategy #1: Strategy #2: Remember to always write your answer in simplest terms. Which of the above strategies do you prefer? _________________________ 5. Simplify each of the following complex fractions using your preferred strategy. If you have time, solve them a second time using the other strategy.
|
||||||||||


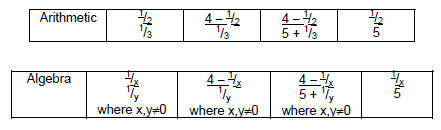
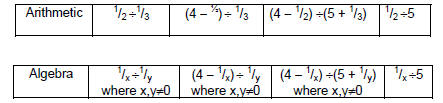
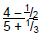 can be rewritten as (4 − 1/2) ÷(5 + 1/3). The
can be rewritten as (4 − 1/2) ÷(5 + 1/3). The